I introduced a Table 1 – Māyā_Dimensions in Appendix 8 . Here I would like to elaborate on this concept and present more details on how this table has come about. In this ‘form’ it does not exist in any present literature and has been actually enthused from a variety of sources/readings both from the western and eastern sides. In establishing this diagram I have tried to bring some method to a very large body of writings and concepts starting with the idea of dimensions from physics and integrating it with the idea of Māyā from early Hindu writings. We must keep in mind that we are stepping out here into ‘something of the Unknown’ and the only reassurance that I have had is that from time to time my various metaphysical and Vedic readings have fitted almost hand in glove with this picture. So, now, I would like to carry you step by step through this journey….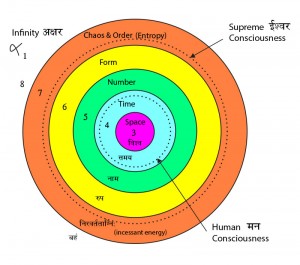The structure shown above is the first blank table that I put together based on the work of two authors, both from the field of parapsychology , attempting to integrate the diverse disciplines of university education into a new order, a novel synthesis :-

(1) Serena Roney-Dougal, a Ph.D in Parapsychology who has written the book “Where Science & Magic Meet” (Element 1991)
(2) Ken Wilber, a prolific spiritual and scientific writer who helped forge the new field of transpersonal psychology. An original thinker whose pioneering work has given him the title of ‘the Einstein of consciousness’. He has more than sixteen books to his credit. His latest is “A Theory of Everything – An integral vision”.

● What is the starting “point” of dimensions? Exactly that, the ‘point’, which geometrically speaking is ‘zero’ dimension. It has no measurement, no length or width or breadth ; it is the bindu of hindu philosophy that which is pivotal to all creation. We have to be careful with terminology here – bindu or ‘point’ is not void or emptiness. It is not the shūnya of Sanskrit. The bindu is a ‘vibrant’ idea ; it may not have spatial dimensions or ‘sides’ to it but it is. This is beautifully explained in an article in Kalātattvakośa [1] from which I excerpt below :

The term bindu , dot, point, spot, drop, semen, can be derived from the verbal root bid, meaning ‘to cleave, to split’. According to the Nirukta it is derived from the verbal root bhid, meaning ‘to pierce’, hence ‘hole’…

According to modern geometry, the point is the minutest unit with which a line is drawn. The point is indivisible and without length and breadth. When we think of bindu as the minutest unity we are reminded of the concept of paramānu ( Vaiśesika defines paramānu as : mūrtatve sati niravayavah : being limited, it is without any body part ).

In Yogabhāsya of Vyāsa we find that a substance when reduced to its minutest unit is called paramānu , and in the same way the minutest time unit is called ksana. But bindu is neither a time unit like ksana nor a space unit like anu ( ANauu ). It is a unit of consciousness , and at the same time becomes body of the material world.

Thus bindu is variously explained in terms of Hindu philosophy. In māyā (Appendix 8), we learnt that the observable universe is a reflection of the mind which is the seat of our individual consciousness.

• • Here we are learning that this very act of observation has a fundamental unit viz.

bindu

We will further see that it is this unit that unfolds into the substantial units of space, time, speech, form and chaos-order. [In fact, we are getting close to some of the ideas of Quantum Mechanics].

● We will now look at some western writers who have talked about the ‘point’ in terms of a deeper meaning. Intuitively, they strike a chord with the eastern idea of the bindu going far beyond the conventional, bland geometrical definition of a ‘point’ :-[2]

◊ Firstly, Thomas Stearns Eliot (1888 – 1965), winner of the 1948 Nobel Prize for literature, whose poems have a spiritual undertone. He was well acquainted with Vedic philosophy and used Krishna and Arjun’s dialogue from the Bhagwadgita in his famous metaphysical poem ‘The Waste Land’. In fact, he concludes it with a quotation from the Brihadarārānyaka Upanishad followed by …..shantih shantih shantih.

I am going to present extracts from Eliot’s Four Quartets, which are brilliant, in that, it takes speech to a higher dimension by structuring a poem as a musical symphony. Further, its central theme is “the union of the flux of time with the stillness of eternity” and, this, the poet calls the ‘still point’. A critique explains [3]:-

The title of the poem is derived from the terminology of music. ‘Quartet means a set of four voices or instruments. Each part of the poem is divided into five movements equivalent to the five musical movements of a symphony : allegro, andante, minuets, scherzo and rondo… Eliot achieved the height of his musical skill in Four Quartets and he, himself, has said in his essay, The Music of Poetry, that poetry maybe benefited by a quantum of musicality in it.

The four parts of Four Quartets are not independent poems because they revolve around the same central theme of time. Therefore, the four parts make a definite pattern which is the unity of the poem. Eliot speaks of two kinds of time : the ordinary fleeting Time, and the eternal Time that he refers to as the ‘still point’ in which past, present and future stand united.

Here, I am going to look at the first, the second and the fifth movements of Burnt Norton – the first poem ; and at the fifth movement of Little Gidding – the fourth poem. However, I have hyperlinked all the Four Quartets in the references. I recommend a guided study using one of the many critiques in print. The idea of ‘eternal children’ silently hidden in the rose garden is taken from a poignant, thought-provoking short story by Rudyard Kipling of a blind English mistress in a large country estate. It is called ‘They’ because the blind lady is aware of the inside and outside of her vast estate in terms of the activity of these children and their giggles and laughter. She always refers to them as ‘they’.
You will see that in Four Quartets Eliot has carried the ‘still point’ beyond ‘fixity’ and enriched it by curling various ‘times’ into it – past, present and future :

“Time past and time future
What might have been and what has been
Point to one end, which is always present.”

And, as if to stress the overlap of the beginning and the end, Eliot uses the same lines to both open and close the Ist movement of ‘Burnt Norton’.  In the same movement, the poet also says:

 “And the pool was filled with water out of sunlight,

And the lotos rose, quietly, quietly,

The surface glittered out of heart of light,

And they were behind us, reflected in the pool.”

Here, Eliot is very close to the Purānic creation myth in which Vishnū, the Sun God & the Preserver gives birth to Brahmā, the Creator riding a lotus emanating from his nābhī or navel. In fact, nābhī is a group word for bindu and is the seat of the third Chakra i.e. the Manipura . And, as the creation happens ‘the pool’ reflects the mayānvi universe.

In the IInd movement of ‘Burnt Norton’ Eliot coagulates space and time into the ‘still point’ of the turning world :

                                    “At the still point of the turning world. Neither flesh nor fleshless;
Neither from nor towards; at the still point, there the dance is,
But neither arrest nor movement. And do not call it fixity,
Where past and future are gathered. Neither movement from nor towards,
Neither ascent nor decline. Except for the point, the still point,
There would be no dance, and there is only the dance.”

Let me cite further from Kalātattvakośa, :-

bindu does not only constitute the thought-element but also serves as the material of all the elements of matter and speech, that is, everything is made of bindu whether it is the physical body or a metaphysical principle. Hence, bindu is the meeting point of spirit and matter.

This is precisely what Eliot is heading towards when he says later in this movement :

                                   “Time past and time future
Allow but a little consciousness.
To be conscious is not to be in time
But only in time can the moment in the rose-garden,
The moment in the arbour where the rain beat,
The moment in the draughty church at smokefall
Be remembered; involved with past and future.
Only through time, time is conquered.”

To summarize so far – bindu arises as a unit of consciousness, it is a thought-element. Now, the dimensions of space, time, speech and form unfold from this ‘unit of consciousness’ and by that we mean that both the beginning and the end of all these aspects, these dimensions are glued together in the idea of bindu.

A vedic text the Ratna-Triya-Parīkṣā [shlöka (70-71)] explains :bindu is ‘universally understood’ – samākhyāto as
(1) ‘essence of speech’ – śabdatattvamghöṣā ( ghösah also means the ‘conchshell’)
(2) ‘word Brahma’ – vāgbrahma
(3) ‘the stable point of the Kundalini ’ – kundalinī dhruvam˙ ( dhruvah is also the name given to the ‘north star’ – the unchanging reference of the night sky )
(4) ‘power of all conscious knowledge’ – vidyā shaktih
(5) ‘the other aspect of all sound – that is – complete silence’ – parā nāda
(6) ‘this great māyā that surrounds us’ – mahāmāyti deśikaih ( deśikaih connotes spatial immediacy )
(7) ‘the unspoilt void’ – vyöman anāhatam˙

You can probably get a feel for the limitation of expression in trying to explain a transcendental concept like bindu . But whatever the level of difficulty the attempt should be made and this is exactly what the shlöka above has done. In the Vth movement of ‘Burnt Norton’ Eliot accomplishes the same feat :

                                                     “Words, after speech, reach
Into the silence. Only by the form, the pattern,
Can words or music reach
The stillness, as a Chinese jar still
Moves perpetually in its stillness.
Not the stillness of the violin, while the note lasts,
Not that only, but the co-existence,
Or say that the end precedes the beginning,
And the end and the beginning were always there
Before the beginning and after the end.”

The reader must note the sentence ‘The stillness, as a Chinese jar still / moves perpetually in its stillness’. The metaphor of the ‘Chinese jar’ is brilliant because this takes us to the external essence of bindu, which is the ensconcing of dimensions.

Again, in the Vth movement of ‘Little Gidding’ Eliot talks of the beginning and end of time, speech :

                                                    “What we call the beginning is often the end
And to make an end is to make a beginning.
The end is where we start from. And every phrase
And sentence that is right (where every word is at home,….)”

and beginning and end of space :

                                                  “We shall not cease from exploration
And the end of all our exploring
Will be to arrive where we started
And know the place for the first time.
Through the unknown, unremembered gate
When the last of earth left to discover
Is that which was the beginning;”

and the last lines of the entire Four Quartets coalesce the form too:

                                                 “All manner of thing shall be well
When the tongues of flame are in-folded
Into the crowned knot of fire
And the fire and the rose are one.”

The Vedic literature too gives some interesting metaphors of the unfolding of dimensions from the bindu :-

(1) Atharva Veda XIX.30.5

When and what caused the Sea to swell into a thunderous, cloud with lightening and rain ?
Thence arose the Golden [5] binduh and from the same source sprang the kushā (sacred grass) [6], symbolic of the first form of life.

(2) Atharva Veda IX.1.21

Here, kashā literally means ‘a horse-whip’ – it also refers to ‘a linking rope’.
antarikś is the vacuum region and it could be either inter-galactic or inter-atomic (for here the prefix antar should be understood as inter- or that which is in between)
dyauh is the border of the ‘deducible’ universe – it is the nominative-singular of the noun div ( idva ) which literally means the ‘region of light’ or the heaven. …therefore this shlöka says :-

The Golden binduh cracks the whip of lightening at the ‘edge of the visible universe’, dyauh,[7] and using the inter-space as the womb creates the earth’s sufferance i.e. gives birth to the ātmic life.

(3) Naiśadh Caritā 1.21

löman is the hair on the body of men and animals, kötibhi is the instrumental-plural of köti or the tip of a point ; here meaning ‘through collecting the tips of the hairs’ roam literally means the ‘soft hair’, kūp means a ‘dark well’; roamkūpö therefore means ‘the skin-pore’ ; miśāh means ‘the blinking of an eye’ and agh is the suffix for impure or sinful ; …therefore this shlöka says :-

How do you cup all the hairs on a person’s body, thereby making their tips form an unbroken line, and then to be able to count this discreteness ?

Its not that this ‘moving universe’ or jagat has been created, in the sinful, blinking of an eye, growing hair-like from the skin-pore ; then how does it emanate – from the disturbance or ruination of the void of binduh?

This last shlöka is brilliant in its metaphors and invokes the idea of infinities without any math! It resonates with the old Greek dilemma – probably best expressed by Euclid (330 – 275 BC) when he tried to answer the question – “How many points are there in a ‘line segment’ ?” Now, a line is a ‘line’; it is continuous and how can we talk about it as ‘discrete’ points ? As we have seen above the eastern philosophy treats both the ‘point’ and the ‘continuous line’ belonging to the realm of brahma, the unknown. Euclid, however, dismisses this and in the very first definition of Elements defines a ‘point’ as – that which has no part [8]. And this is the beginning of geometry. Truly speaking, this was the start of Linear mathematics that has been built meticulously on such idealistic definitions and principles. Over the centuries, as various paradoxes emerged the western mind began looking at what they call Non – linear mathematics. As we will see, the practical Universe also lends itself more favourably to the latter approach. On the other hand, the eastern mindset first looked at the Universe and its rhythms and then built a language Prākrit (Sanskrit’s mother language), based on these resonances called shrutīs.
◊◊ F. Doestovsky explains this succinctly in “The Brothers Karamazov” while explaining his idea of God to his brother Alyosha, “as stupidly as he could” goes directly to the truth of things because “while intelligence wriggles and hides itself…. stupidity is honest and straightforward”. He first expresses his dilemma – “Yet there have been and still are geometricians and philosophers, and even some of the most distinguished, who doubt whether the whole universe, or to speak more widely, the whole of being, was only created in Euclid’s geometry; they even dare to dream that two parallel lines, which according to Euclid can never meet on earth, may meet somewhere in infinity. I have come to the conclusion that, since I can’t understand even that, I can’t expect to understand about God”. And then he concludes – “I believe in the underlying order and the meaning of life; I believe in the eternal harmony in which they say we shall one day be blended. I believe in the Word to Which the universe is striving, and which Itself was ‘with God,’ and Which Itself is God and so on, and so on, to infinity”…….. “Let me make it plain. I believe like a child that suffering will be healed and made up for, that all the humiliating absurdity of human contradictions will vanish like a pitiful mirage, like the despicable fabrication of the impotent and infinitely small Euclidian mind of man, that in the world’s finale, at the moment of eternal harmony, something so precious will come to pass that it will suffice for all hearts, for the comforting of all resentments, for the atonement of all crimes of humanity, ….”

◊◊◊ Galileo Galilei (1564 – 1642) addressed these paradoxes of the continuum with great insight –
(1) the paradox of two concentric circles having the same number of infinite points, is covered in Chap.1 on Infinities.
(2) we cover here his paradox of the ‘point and the round razor’. The text is hyperlinked. Galileo constructed a cylinder with the same height as its radius and then embedded two geometrical figures in it as shown separately in Fig.1

The cone shown in red uses the same base as the cylinder and its peak rises to the centre-point of its top surface. The hemisphere shown in blue ‘cups’ into the cylinder touching its base at the centre-point of the bottom surface. If ‘ r ’ is the radius of the base, then by definition ‘ r ’ is also the height and the volume of the cylinder = π r³. That of the cone is (⅓ base x height) = ⅓ π r³ ; the hemisphere’s volume is ⅔ π r³.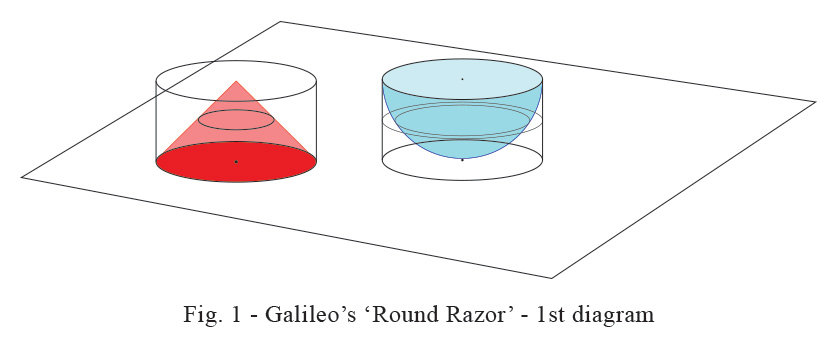

Galileo compared the ‘cone’ shown in red with the ‘bowl’ i.e. the volume of the cylinder in the second figure with the blue hemisphere scooped out. Now, both these geometrical figures have the same volume viz. ⅓ π r³.

If now we ‘cut’ this cylinder at any place in between its height we cut the ‘cone’ in a smaller circle and the ‘bowl’ in an annular ring as shown in Fig.2 below :-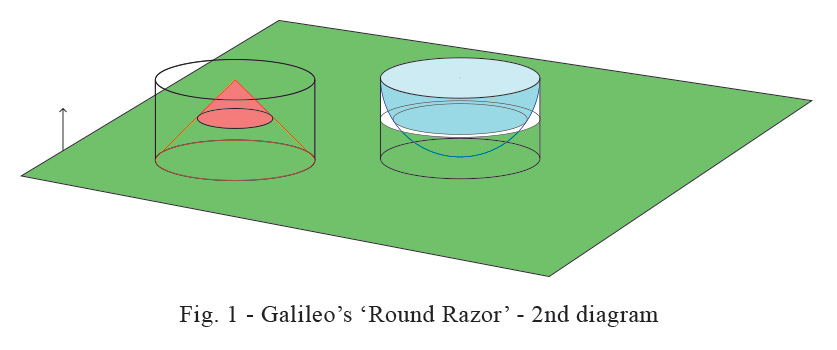Then geometrically the area of the smaller circle is the same as that of the annular ring. The simple geometrical proof is given in the attached article. In Galileo’s words :-

And as the cutting plane (here shown in green) moves upwards, coming near the top, the two solids (always equal) as well as their bases (areas which are also equal) finally vanish, one pair of them degenerating into the circumference of a circle, the other into a single point, namely the ‘round razor’- the upper edge of the bowl and the ‘apex’ of the cone. Now, since as these solids diminish equality is maintained between them up to the very last, we are justified in saying that, at the extreme and final end of this diminution, they are still equal and that one is not infinitely greater than the other. It appears therefore that we may equate the circumference of a large circle to a single point. And this which is true of the solids is true of the surfaces which form their bases ; for these also preserve equality between themselves throughout their diminution and in the end vanish, the one into the circumference of a circle, the other into a single point. Shall we not call them equal seeing that they are the last traces and remnants of equal magnitudes ?

Note also that, even if these vessels were large enough to contain immense celestial hemispheres, both there upper edges and apexes of the cones therein contained would always remain equal and would vanish, the former into ‘round razors’ having the dimensions of the largest celestial orbits, the latter into single ‘points’. Hence, in conformity with the preceding we may say that all circumferences of circles, however different, are equal to each other, and are each equal to a single point.

And in answer to Euclid’s question of the ‘number of points in a line ?’ Galileo concludes:-
…..I shall ask you to tell me whether, in your opinion, a continuum is made up of a finite or of an infinite number of finite parts….My answer is that their number is both infinite and finite ; potentially infinite before division and actually finite after division ; because parts cannot be said to exist in a body which is not yet divided or at least marked out…..I think there is, between finite and infinite quantities, a third intermediate term which corresponds to every assigned number…..I grant, therefore to the philosophers, that the continuum contains as many finite parts as they please and I concede also that it contains them, either actually or potentially, as they may like…

◊◊◊◊ The amazing Argentinian writer Jorge Luis Borges [pronounced Bŏrhez](1899 – 1986) sums up our musings, so far, in an interesting short story titled ‘The Book of Sand’[12]….. He comes to the point right at the beginning “The line is made up of an infinite number of points; the plane of an infinite number of lines; the volume of an infinite number of planes; the hypervolume of an infinite number of volumes……No unquestionably this is not – more geometrico – the best way of beginning my story.”
Borges uses the metaphor of an infinite book acquired by a salesman from India whose pages are uncountable like grains of sands….

“ ‘ I acquired the book in a town out on the plain in exchange for a handful of rupees and a Bible. Its owner did not know how to read. I suspect he saw the Book of Books as a talisman. He was of the lowest caste; nobody but other untouchables could tread his shadow without contamination. He told me his book was called the Book of Sand, because neither the book nor the sand has any beginning or end.’

The stranger asked me to find the first page.

I laid my left hand on the cover and, trying to put my thumb on the flyleaf, I opened the book. It was useless. Every time I tried, a number of pages came between the cover and my thumb. It was as if they kept growing from the book.

‘Now find the last page.’

Again I failed. In a voice that was not mine, I barely managed to stammer, ‘This can’t be.’
Still speaking in a low voice, the stranger said, ‘It can’t be, but it is. The number of pages in this book is no more or less than infinite. None is the first page, none the last. I don’t know why they’re numbered in this arbitrary way. Perhaps to suggest that the terms of an infinite series admit any number.’ ”

Borges touches upon space and time when he says…

“If space is infinite, we may be at any point in space. If time is infinite, we may be at any point in time.”

The author’s dilemma of analyzing this Book of Sand leads him to insomnia and he keeps looking for patterns until he realizes that there is no end to infinite possibilities. He then just ‘loses’ the book in a library.

◊◊◊◊◊ Few decades later, John Milton (1608 – 1674) as if gazing through Galileo’s invention, the telescope, wrote in ‘Paradise Lost’ :-[13]

The golden Sun in splendor likest Heaven
Allur’d his eye : Thither his course he bends
Through the calm Firmament ; but up or downe
By center, or eccentric, hard to tell,
Or Longitude, where the great Luminarie
Alooff the vulgar Constellations thick,
That from his Lordly eye keep distance due,
Dispenses Light from farr ; they as they move
Thir Starry dance in numbers that compute
Days, months, and years, toward his all-chearing Lamp
Turn swift their various motions, or are turnd
By his magnetic beam, that gently warms
The Univers, and to each inward part
With gentle penetration, though unseen,
Shoots invisible virtue even to the deep :
So wondrously was set his Station bright.
Their lands the Fiend, a spot like which perhaps
Astronomer in the Sun’s lucent Orbe
Through his glaz’d Optic Tube yet never saw……

Here, the poet gazing at ‘the calm Firmament’ and its ‘center, or eccentric, hard to tell’ outlines the Lordly assignations between these two limits.

● And now we will see how bindu addresses this duality of nature :-

(1) We first look at the Brahmabindu Upanisad which literally means “esoteric instruction on the bindu that signifies the (higher) Brahman” [14]. In the first shlöka the duality is said to emanate from the mind – the very seat of consciousness :-

The Mind, they say, is twofold, either impure or pure.
Impure, when it imagines desires; Pure, when it is free from desires.

The connotation is that desire is the first disturbance in consciousness and this can have two aspects, viz. desire in which the mind is involved, and the other is, desire in which the mind is not involved. So here this shlöka is pointing towards the idea of niśkāmkarm, or action without worrying about its fruit or end-result. We can also see the first hint of the ‘order-disorder’ dichotomy. (note: talk about ‘rhythms of nature’)[15]

The literal word for dimension in Sanskrit is parimāṇ ( pirmaaNa ) . The suffix pari ( pir ) means ‘extensive’, ‘surrounding’ or in terms of quantity ‘substansive’ and mā again is ‘measure’. Thus parimān could apply to space, weight or in general to any measurable entity and this is to be achieved by division.
This is a natural stop for ‘Dimension – I’. We will look at the unfolding of the dimensions in the next talk and see how the concept of bindu first leads us to a duality and then a multiplicity that eventually encompasses this entire conscious universe – the māyā .