The Shāntī Pāth & Cantor’s Infinities
Millions of Indians chant the Shāntī Pāth or the peace invocation daily at the beginning and end of every satsangh, literally a gathering of truth-seekers. Such gatherings are commonplace among the populace where thousands assemble to listen to vedic discourses from Gurus of their choice. The Shāntī Pāth is placed at the beginning of the Iśavāsya Upanishad and in its extended form is the first shlöka of the 5th Adhyāy of the Brihadaranayak Upanishad .
! PaUNa-ma\ Ad:, PaUNa-ma\ [dma\ , PaUNaa-t\ PaUNa-ma\ ]dcyato.
PaUNa-sya PaUNa-ma\ Aadaya , PaUNa-ma\ eva AvaiSaYyato .
! Saaint: Saaint: Saaint:.
pūrnam adah, pūrnam idam, pūrnāt pūrnam udacyate
pūrnasya pūrnam ādāya pūrnam evāvaśisyate.
For our purpose here we take S.Radhakrishnan’s[1] explanation :
That is full, this is full. From fullness fullness proceeds.
If we take away the fullness of fullness, even then fullness remains.
Aum (the syllable) is Brahman (who) is the ether, the primeval ether….
Swami Chinmayanandji[2] explains it as follows :
That is Whole; this is whole; from the Whole the whole becomes manifest.
From the Whole when the whole is negated what remains is again the Whole.
Paul Deussen[3] translates it as:
That is perfect and this is perfect, out of the perfect, the perfect one is created.
If one takes out the perfect from the perfect, there still remains the perfect.
Om ! the expanse is Brahman, the wide expanse; the primaeval airspace filled with expanse !….
‘The Brhadāranyaka Upanisad’ by Ramakrishna Math is more explicit in its translation:
Om That (Brahman) is Infinite, this (universe) too is infinite. The infinite (universe) emanates from the Infinite (Brahman).
Assimilating the infinitude of the infinite (universe), the Infinite (Brahman) alone is left.
Om is the ether-Brahman – the ether that is eternal….
The word pūrna [4] has been variously translated above as full, whole, perfect and infinite. pūrna = pūr + kta[5] here pūr is the root that signifies fullness or completeness; the suffix kta is used to further stress this completion. In other words pūrna stands for something that is more than complete or beyond are imagination!
The interesting dichotomy of the dual usage of this word stresses the fact that there are further two levels of completeness that exceed our mental capacity; there is an inherent limitation. In the words of Swami Chinmayananda [6] –“This peace invocation reads as though a pleasant contradiction in terms. On a very superficial reading one is apt to consider only its word-meaning and then each sentence should certainly confuse and confound any modern student who dives into it especially through its literal translations available for him in English or in any vernacular. This is a philosophical truth-declaration, and as such unless we know something of Vedantic conclusions over the theme of the transcendental Infinite and its ‘relationship’ with the finite, this stanza should necessarily confuse any reader.”
On the mathematical side in 1870, Georg Cantor (1845 – 1918) gave us the ‘set theory’ – a brilliant thesis on the study of collections of numbers, points, objects, anything really in general. This revolutionized ‘number theory’ and gave rise to his– ‘Theory of Infinities’ or what is more precisely called ‘Cantor’s theory of Trans-infinite cardinals’. The word trans-infinite here maybe understood as a condensed form of transcendental Infinite – that which is beyond the infinite. How is this possible ? Let us, at this point, push our limited reasoning on the lines of Cantor and attempt to explain this brilliant equivalence between – mantra and math – separated by almost four millennia of human endeavor !
The ‘lazy eight’ symbol ‘∞’ has long been used to denote the infinite since this shape can be traversed endlessly.
Till the mid 19th century, the only concept of infinity, in the mathematical world, was linked to ‘countable numbers’ or integers or natural numbers – as they are commonly known. As we count, we go :
1, 2, 3, 4,…..n…….. ∞
Here ‘n’ stands for any countable integer. At the end of this seemingly endless sequence, the number becomes too large to count and is denoted by ‘∞’.
The earliest limitation of this way of thinking was probably expressed by Euclid (330 – 275 BC) when he tried to answer the question – “How many points are there in a ‘line segment’ ?” Now a line is a ‘line’; it is continuous and how can we talk about it as ‘discrete’ points ? But then, that is what mathematicians are all about; they question what seems obvious and keep building a pyramid of well-grounded higher knowledge. In fact Euclid’s axioms and theorems are even today part of elementary school Geometry. But he could not answer this one!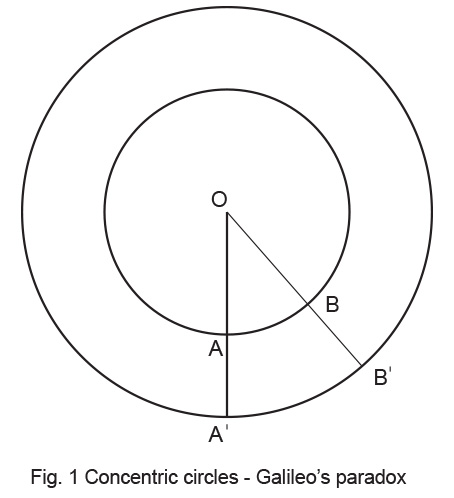 Galileo Galilei (1564 – 1642) published in 1638 Dialogue of the Two New Sciences gives some excerpts of his arguments on this). In this work, he outlined a paradox relating to ‘natural numbers’ and their ‘squares’. He derived a geometric equivalent by arranging two concentric circles as shown in Fig. 1. and raised the question– “Are the number of points on the inner, smaller circle the same as those on the outer, bigger one ?” For every point A or B on the inner circle, there is a corresponding ray OA or OB respectively and a corresponding A’ or B’ point on the outer circle and so on. Thus, infinite rays emanate from ‘one’ center O. These diverge to an infinite number of points A,B etc. on the smaller circle and each in turn connects to a corresponding A’, B’ etc. on the outer one. The paradox explicitly is – “how can the rays emanating from the center link an identical number of infinite points on the inner and outer circle ?” The answer to our question is not obvious and it did trouble intellectuals for almost three centuries till Cantor resolved it rigorously.
Galileo Galilei (1564 – 1642) published in 1638 Dialogue of the Two New Sciences gives some excerpts of his arguments on this). In this work, he outlined a paradox relating to ‘natural numbers’ and their ‘squares’. He derived a geometric equivalent by arranging two concentric circles as shown in Fig. 1. and raised the question– “Are the number of points on the inner, smaller circle the same as those on the outer, bigger one ?” For every point A or B on the inner circle, there is a corresponding ray OA or OB respectively and a corresponding A’ or B’ point on the outer circle and so on. Thus, infinite rays emanate from ‘one’ center O. These diverge to an infinite number of points A,B etc. on the smaller circle and each in turn connects to a corresponding A’, B’ etc. on the outer one. The paradox explicitly is – “how can the rays emanating from the center link an identical number of infinite points on the inner and outer circle ?” The answer to our question is not obvious and it did trouble intellectuals for almost three centuries till Cantor resolved it rigorously.
Cantor carried the concept of the ‘countable infinity’, which he termed א0 (Aleph – nought) to the ‘indenumerable infinity’ which he named א1 (Aleph-one). [A very readable account of Cantor’s work is given in ‘Fractals – Images of Chaos’ [7]]. Note here that the description ‘countable infinity’ also means ‘that which in principle can be counted’ and it can also be termed as ‘denumerable infinity’.The ‘indenumerable infinity’, א1 is likened to ‘that which cannot be counted’ and is part of the continuum. Cantor developed ‘degrees of infinities’ between א0 to א1 by using one-to-one correspondence between the elements of two sets.
- e.g. What do we make of the statement : There are as many even (or odd) numbers as there are natural numbers ? There are infinitely many of each sort and at first it seems that the even(or odd) numbers appear alternatively and therefore should be less than the natural numbers…but it is not so…for we can match them as follows :
 We see the one-to-one correspondence between the two sets and we conclude that since every number has its match – both the sets approach the same degree of infinity – in this case א0.
We see the one-to-one correspondence between the two sets and we conclude that since every number has its match – both the sets approach the same degree of infinity – in this case א0.
Now, for the next statement : The number of squares equals the number of all the natural numbers. This seems odd, because as we continue in the series of all the natural numbers ..See Fig. 3 below
 the squares (underlined) occur less and less often. Still if we use Cantor’s matching principle of set theory we find :
the squares (underlined) occur less and less often. Still if we use Cantor’s matching principle of set theory we find :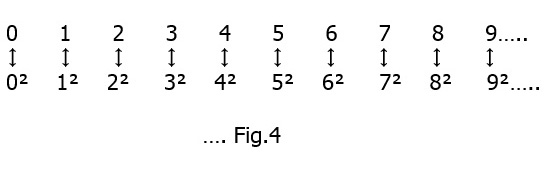 that the ‘infiniteness’ of the ‘square numbers’ corresponds one-to-one to the degree of infinity of the natural numbers which is the ‘countable infinity’ or א0. In the same way it can be shown that the set of all third powers, or any higher power, also tends to the same ‘countable infinity’. Thus if we can find a unique way to match any set to the natural numbers one-to-one the degree of infinity in the end remains the same viz. א0.
that the ‘infiniteness’ of the ‘square numbers’ corresponds one-to-one to the degree of infinity of the natural numbers which is the ‘countable infinity’ or א0. In the same way it can be shown that the set of all third powers, or any higher power, also tends to the same ‘countable infinity’. Thus if we can find a unique way to match any set to the natural numbers one-to-one the degree of infinity in the end remains the same viz. א0.
This helped Cantor resolve the Galileo’s paradox stated above – the number of points on the center, the smaller circle or any bigger circle all belong to ‘countable infinite’ rays.
- As we said earlier, Cantor pushed his mathematical reflections on set theory and the ‘infinitely many’ further. He showed that there exist sets with an ‘infiniteness’ which is ‘beyond countability’ i.e. these sets have a degree of infinity that is higher than א0!
For this purpose, Cantor used a line segment as a measure for ‘real numbers’. Whereas ‘natural numbers’ belong to the sequence 0, 1, 2, 3, 4, and so on, the ‘real numbers’ are those which are integers with a decimal placed between them somewhere e.g. 1.291 or 0.3125 or 365.89 and so on and so forth. These are also known as decimal numbers. In real life, we use ‘real numbers’ for measurements, weights, scientific calculations, cash transactions etc.
René Descartes (1596 – 1650) developed the idea of graphical representation, whereby, he represented ‘real numbers’ by the length of a line and accordingly defined a co-ordinate system. Thus a horizontal line can represent ‘real numbers’ from zero onwards. See Fig.5 below : Next let us look at ‘fractions’. By a ‘fraction’ we mean ‘the ratio of two natural numbers’ e.g. 1:4, 2:7, 1:125, 23:2365, ……. and so on. Fractions are also called ‘rational numbers’.[8]
Next let us look at ‘fractions’. By a ‘fraction’ we mean ‘the ratio of two natural numbers’ e.g. 1:4, 2:7, 1:125, 23:2365, ……. and so on. Fractions are also called ‘rational numbers’.[8]
By contrast , there are irrational numbers, like P, √2, √3 etc.[9] When we express these decimals they are infinitely long.In other words the decimal expansion of ‘irrational numbers’ neither terminates nor is periodic; it extends interminably e.g. P = 3.14159…. computers have checked it to a million decimal places without it ending or repeating.
‘Rational numbers’ always terminate or give a periodically recurring decimal. Conversely, a recurring or exact decimal will always be a fraction.
Now we make a very surprising statement : There is the same number of fractions as natural numbers ! Cantor made a grid as follows:-
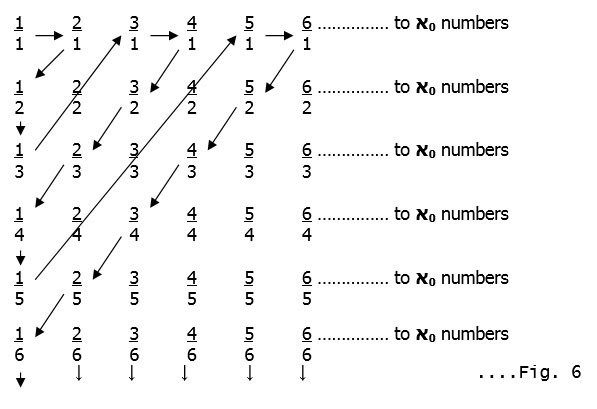 If we follow the arrows in Fig.6 as shown (and skip the common fractions like 1:1 is the same as 2:2 or 3:3 and so on ; 2:1 is the same as 4:2 or 6:3 and so on and so forth)
If we follow the arrows in Fig.6 as shown (and skip the common fractions like 1:1 is the same as 2:2 or 3:3 and so on ; 2:1 is the same as 4:2 or 6:3 and so on and so forth)
we can again use the correspondence principle used earlier. Number each arrow-stop using the natural numbers :-
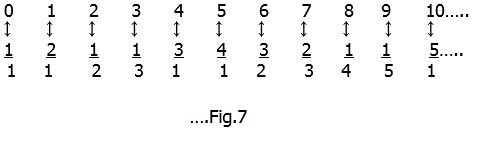 Each fraction has a ‘unique’ natural number associated with it and the entire grid can thus be covered exhaustively. Both sets therefore have the same ‘infiniteness’, that is they are both ‘countably infinite’ and have א0 elements.[10] These concepts and others are explained in greater mathematical detail by Rudy Rucker[11] and Paul Davies[12].
Each fraction has a ‘unique’ natural number associated with it and the entire grid can thus be covered exhaustively. Both sets therefore have the same ‘infiniteness’, that is they are both ‘countably infinite’ and have א0 elements.[10] These concepts and others are explained in greater mathematical detail by Rudy Rucker[11] and Paul Davies[12].
- If we think of the rational numbers, say just between ‘0’ and ‘1’ (we can also write this as [0,1] ) , and arrange them by size, it seems this interval is completely filled by these fractions. But this is not so, between two rational numbers, however close, there will always be another rational number. To appreciate this take
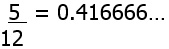 (here the 6 recurs endlessly and we can write instead 0.41‾6) 12
(here the 6 recurs endlessly and we can write instead 0.41‾6) 12
and we take the fraction ![]() (here the entire sequence 428571 cycles)
(here the entire sequence 428571 cycles)
We can make a new fraction in between these two rational numbers by adding both the numerator and denominator together as follows :-
 It looks as if the rational numbers fill the interval [0,1] completely. However, this is not so. There are irrational numbers between the fractions everywhere. Oddly there are “many more” irrational numbers than fractions. Cantor’s great discovery was that the set of all decimals (i.e. all rational and irrational numbers) is ‘uncountably infinite’. This ‘uncountable infinity’ he called א1 and demonstrated that it is ‘bigger’ than the ‘countable infinity’, א0.
It looks as if the rational numbers fill the interval [0,1] completely. However, this is not so. There are irrational numbers between the fractions everywhere. Oddly there are “many more” irrational numbers than fractions. Cantor’s great discovery was that the set of all decimals (i.e. all rational and irrational numbers) is ‘uncountably infinite’. This ‘uncountable infinity’ he called א1 and demonstrated that it is ‘bigger’ than the ‘countable infinity’, א0.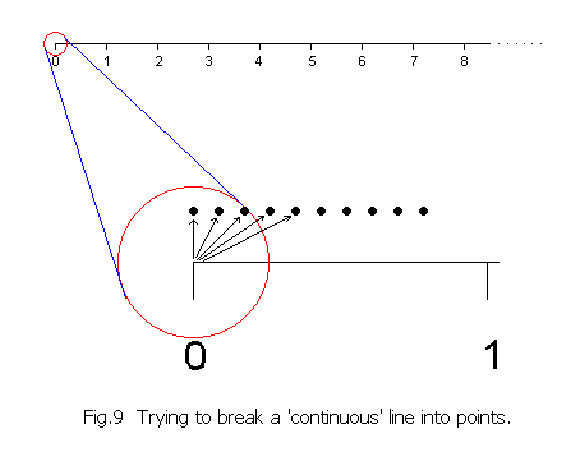 Now, let us go back to the continuous line of Fig.5 and imagine attempting to dismember it by taking the points, one by one, from the left end and arranging them in a row individually as shown in Fig. 9:-
Now, let us go back to the continuous line of Fig.5 and imagine attempting to dismember it by taking the points, one by one, from the left end and arranging them in a row individually as shown in Fig. 9:-
Even after removing an infinity of points, the line has not shrunk by the smallest of distance, for these isolated points, each of “zero” length, can never accumulate to measure any length at all. (Mathematically a point is defined as “zero dimension” i.e a natural number however large, will give a non-existent product when multiplied by its “zero” length.) Similarly, an א0 infinity of isolated points will always remain countable. If they are shrunk down together without limit, they can never fill out even the shortest part of a continuous line. The infinity associated with ‘continuity’ is of a ‘higher nature’ ! It is ‘uncountably infinite’.
Proving this seems difficult at first, but Cantor’s reasoning was so simple and original that it is worth understanding it. His is a ‘proof by contradiction’. Here we start with a statement that is opposite of what we want to prove and then show that this leads to an inconsistency.
- Let us take the entire set of decimal numbers i.e. all the numbers between [0,1]. This means that the rational and irrational numbers are in this together. And we know that the fractions or the rational numbers are ‘countably infinite’.
The essence of Cantor’s proof is that we assume that the decimals (irrational & rational numbers both put together) are as numerous as the natural numbers ( i.e. integers, and we have shown above that the rational numbers have the same infinity א0, as the integers themselves) then it should be possible to label them one by one.
Let us accordingly number the list a1, a2, a3, a4 and so on :-
 We imagine each a1, a2, a3 etc. to be a decimal number that continues indefinitely. In case it terminates (i.e. it is rational and is an exact fraction) then we will fill up the digits with zeros.
We imagine each a1, a2, a3 etc. to be a decimal number that continues indefinitely. In case it terminates (i.e. it is rational and is an exact fraction) then we will fill up the digits with zeros.
This means that all the decimals are listed out exhaustively in an infinite column (the labeling can be random ; one such ordering is shown in Fig.10). We next construct a new decimal number ‘b’ as Cantor pointed out – take the first digit of a1 and change it to obtain the first decimal of ‘b’ ; then take the second digit of a2 and alter it to get the second decimal of ‘b’ and so on move diagonally down the entire infinite column.[For mathematical precision the changed digits should not be either 0 or 9].
A possible ‘b’ from Fig.10 could be :-
 But, if our original list is complete then ‘b’ should be in it somewhere. The way Cantor constructed ‘b’ he ensured that it has at least one decimal digit different from each one of the ai’s . For example, if we say that an (‘ai’ with the nth index) is the same as ‘b’ – it cannot be so since the nth decimal of ‘an’ and ‘b’ are different by Cantor’s process of inception. Thus, a contradiction has arisen in our initial assumption. Therefore, the decimal numbers are ‘uncountably infinite’ and this infinity, א1 (Aleph – one) is higher than the ‘countable infinity’, א0 (Aleph – nought).
But, if our original list is complete then ‘b’ should be in it somewhere. The way Cantor constructed ‘b’ he ensured that it has at least one decimal digit different from each one of the ai’s . For example, if we say that an (‘ai’ with the nth index) is the same as ‘b’ – it cannot be so since the nth decimal of ‘an’ and ‘b’ are different by Cantor’s process of inception. Thus, a contradiction has arisen in our initial assumption. Therefore, the decimal numbers are ‘uncountably infinite’ and this infinity, א1 (Aleph – one) is higher than the ‘countable infinity’, א0 (Aleph – nought).
We go back to our original shlöka, the Shāntī Pāth and rewrite it using Cantor’s terminology as :-
Om That (Brahman) is א1, this (universe) is א0. The א0 (universe) emanates from the א1 (Brahman).
Assimilating the infinitude of the א0 (universe), the א1 (Brahman) alone is left.
What at first reading of the Shāntī Pāth sounds like a quibble on the word pūrna or ‘whole’ actually turns out to be a mathematically significant statement. It reflects on the very nature of continuity and its relationship with discreteness. The pūrnam adah is the Supreme Brahman, the integral whole that is paripūrna , attribute less and immutable. The pūrnam idam is also an infinity but like א0, it is quantifiable. The human intellect by its very process of comprehension relegates the Unknowable to an erudite graininess. This in essence is the very basis of Quantum Mechanics and Heisenberg’s principle. The pūrnam adah is the א1 the incomprehensible, unchangeable infinity that can give rise to as many א0s as desired and yet not be exhausted. Cantor used the rules of contradiction to show this. And similarly we have the neti – neti explanation in Brhad. Upanishad II.3.6 – Now therefore there is the teaching, not this, not this for there is nothing higher than this, that he is not this. Now the designation for him is the truth of truth…. S. Radhakrsihnan1.
A similar interpretation for the Shāntī Pāth is given in ‘Kalātattvakośa’[13] :-
Here the word pūrna refers in symbolic terms to the Supreme Reality which, remaining ever immersed in its integral nature, is always self resting. Gopinath Kaviraj has shed light on the sublime philosophical meaning underlying this verse which maybe summarized as follows. This verse attempts to bring out the nature of the Supreme Brahman in terms of the integral Whole which, as such, is beyond finite mind’s comprehension. It is always Full-in-Itself, the one without a second, and therefore suffer from any want or deficiency. It exists everywhere and at all times as the ‘one Whole’, the integral Reality. Being the sole Reality, it is the locus of both creation and dissolution of the world which is going on from time immemorial in the form of the play of its innate power, without affecting in the least its essential integral Nature. Looking from the mundane level, it has two aspects – the aspect which is capable of being apprehended by the mind denoted by the term idam, and the aspect which is beyond the reach of the mind that is indicated by the word adah . But, as a matter of fact, there is no difference whatsoever between these two aspects, because what once appears as within the reach of the senses due to the expansion of one’s capacity may well go out of one’s grasp when the powers of senses contract. It is beyond mutation or evolution. It is formless yet with form, attribute-less yet with all attributes, far yet near, all-pervasive yet transcendent. All contradictions lose their identity in it. All that emerges from It is also of the nature of all-inclusive Fullness. It may be likened to zero which symbolizes the infinity in the domain of mathematics. Any addition or subtraction does not make any change in it. It ever remains the immutable infinity. Thus the Supreme Reality is integral Fullness which is a corollary of its self-resting nature as the Absolute.
In an identical vein Ecclesiasticus XLII. 21-22 expresses:-
He is from Eternity to Eternity, and to Him nothing may be added
Nor can He be diminished, and He hath no need of any counselor.
Corollary 1 – Quantum Mechanics
A brief digression into the history of QM to prepare the reader because a few metaphysical concepts would be in order at this juncture.
In the late 19th century, Max Plānck (1858-1947) was studying the radiation of energy from spherical bodies made of different metals[14]. As these spheres were heated to higher and higher temperatures, they radiated heat waves and became incandescent. All these waves were found to be of electro-magnetic nature, as James C. Maxwell (1831-1879) had shown decades earlier. This research was known as ‘the Black-body radiation’.
Till Plānck researched this problem, earlier theories had given impractical results. They were all leading to mathematical calculations resulting in these heated spheres emanating infinite energy. The experiments, however, did not tally with this. Empirical measurements always gave limited energy values spread over a finite range of heat/light frequencies (or electro-magnetic waves). Plānck had a brilliant insight. He assumed that the energy waves left the ‘Black-body’ in discrete packets and not continuous waves as previously thought. He called these limited packets of energy quanta. They were also later termed as photons since the radiating body also emitted light. This new assumption lead Plānck to a mathematical formulation[15] that corroborated precisely with the observed experimental data.
Albert Einstein (1879-1955) built further on this pivotal idea and it led him to the discovery of the photo-electric effect in 1906. In fact this work got Einstein his Nobel Prize. He showed that the reverse of Plānck’s hypothesis of energy quanta is also true. Light shining on certain sensitive metals generates a small electric current in them. This current varies not with light intensity but with changing light frequency. Mathematically, Einstein showed that light is absorbed too in discrete amounts or quantum packets of energy, and these were the same photons of Plānck’s Black-body radiation.
As the work progressed in early 1900s, light was established to have a dual nature. This came to be known as the wave-particle duality and initially was a very confusing concept. Neils Bohr, one of the co-founders of the atomic theory, accepted this duality and extended it to the ‘electron’[16]. He considered the Hydrogen atom and its light-emission spectrum. The discrete lines of different light frequencies in this spectrum pointed towards discrete energy levels for the planetary electron orbiting the hydrogen nucleus. This was like saying that a planet can orbit the sun in a specific orbit only with all other possibilities being forbidden or out of bounds. Bohr further showed that the ‘electron’ is not only particle–like in its behavior but it has wave-like characteristics too under certain conditions. In the case of the Hydrogen atom the electron assumes only those orbits which are integral multiples of its natural ‘wave-length’, λe. That is it accepts only those orbits which have circumferences of ‘n’ times λe where n= 1,2,3 and so on. This theory gave a brilliant first correspondence to the energy levels experimentally observed in the hydrogen spectrum and this hypothesis gave rise to atomic Quantum Theory, rest is history. Schrödinger, Dirac, Pauli, Heisenberg and many other minds contributed in quick succession to cement this theory into one of the major scientific breakthroughs of 20th century.
Werner Heisenberg (1901-1976) gave his famous Uncertainty Principle based on this overlapping concept of wave-particle duality. He showed that all matter behaves sometimes as a wave and at other times as a particle. It is the very process of observation which determines which aspect of matter is revealed to us the Observer. As long as the entity is not disturbed it behaves like a wave. The moment we try and pin-point it the particle nature pops up. This switching of nature is significant at the atomic level and lends itself to an Uncertainty in measurement during experiments. It limits our capability of knowing exactly either the position or speed of the particle. The precision in trying to locate the spot at which the atomic entity is results in indeterminacy in knowing how fast it is moving – we cannot measure both aspects with infinite precision. The everyday billiard-ball concept of the particle literally goes out of the window. It has to be replaced by a fuzzy cloud of mathematical probability.
The spatial picture is therefore diffused and dual. Heisenberg’s principle in essence shows that the Observer (and his consciousness) is an integral part of any quantum level experiment. Truly speaking our consciousness cannot ‘know’ the ‘Unknown’ in its entirety. Our experiments, when repeated umpteen times, can only give us probabilistic, time-tested answers.
This is where the modern day Metaphysics began…


